

If it is, that means n has a factor that isn't 1 (it started from 2) or itself (it ends at the square root of itself, and 1 is not an exception because that was fixed with the if n<2 condition). In the loop, I check if i (the loop counter) is divisible into n. The +1 is for keeping the range in bounds if the int() made it less than it was before. The reason for math.sqrt is that n can only have factors until its square root (and also itself).
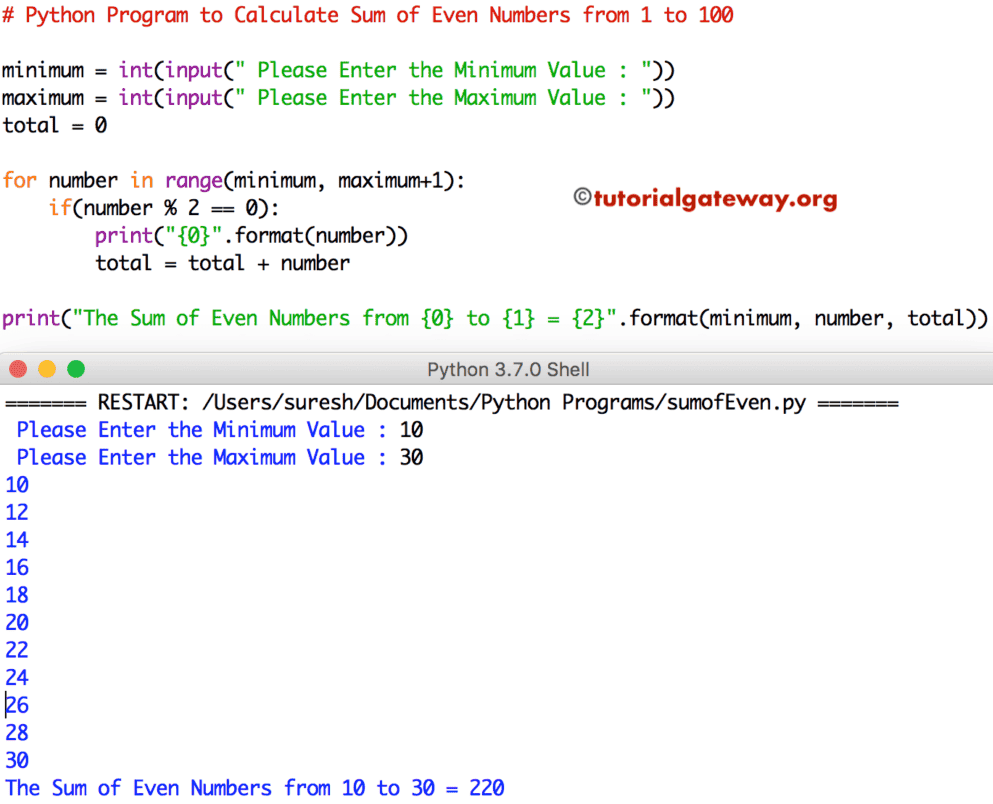
That's just convert math.sqrt(n) into an int, and then add 1. if n<2:Īfter that, I loop from 2 to int(math.sqrt(n))+1. If n-1 (because it was absolute valued) the condition n<2 will suffice. Here it is: from math import sqrt # you can just import math, but I only use sqrt

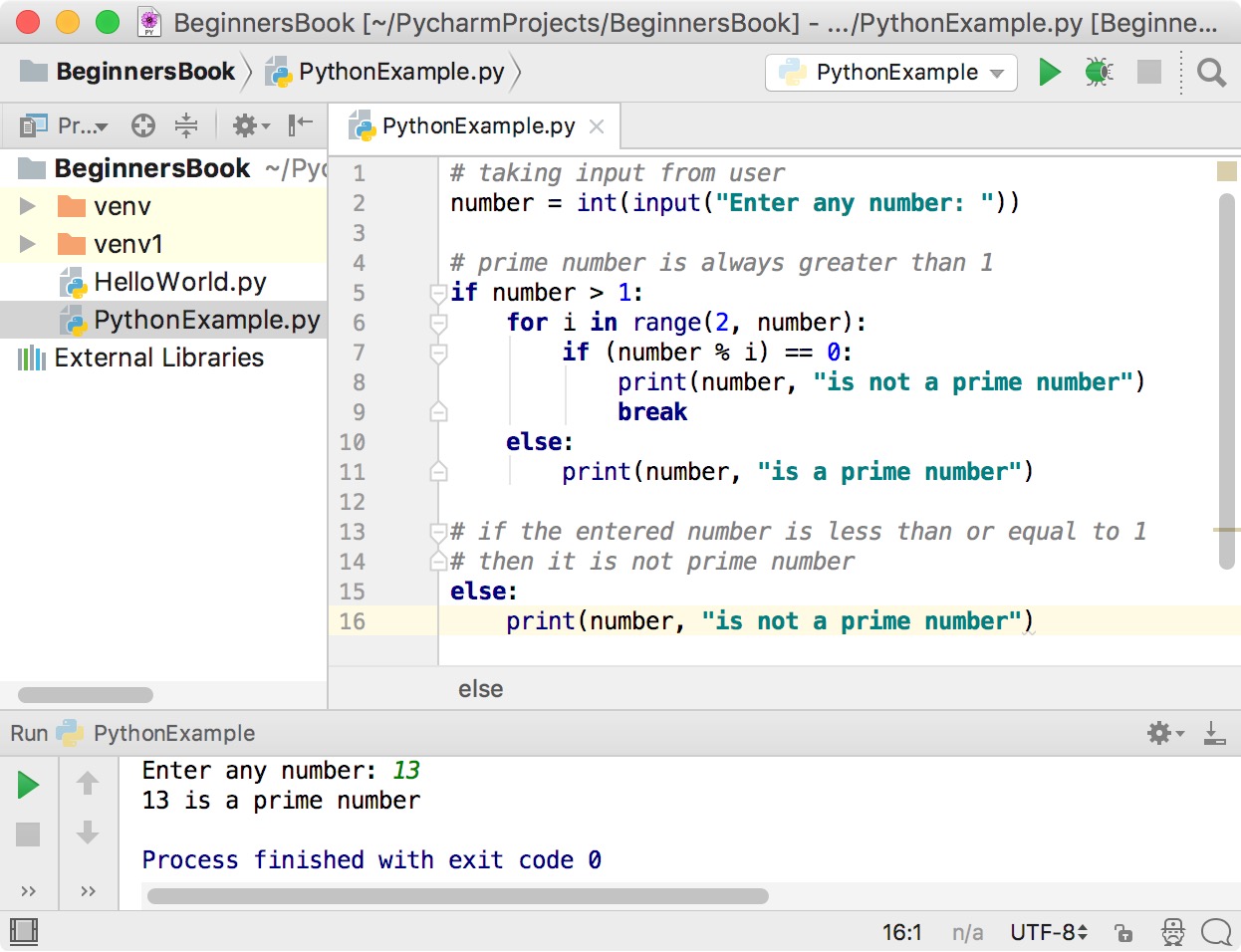
I took some time to develop a quick but accurate is_prime function in Python. You only need to check factors up to the square root of the number.Įdit: I see in your question you mentioned this, you just need to modify this code to return True or False def isPrime(num): You need to sort out the two else statements, and also change the algorithm so that it only prints num is a prime number if all the iterations of the for loop fail if num < 2: # catch 1 and anything less than zero


 0 kommentar(er)
0 kommentar(er)
